18 jun 06
"what is the solution to the Riemann hypothesis?"
now, i know this is some not-yet-solved math problem. actually, it's a hypothesis, someone's idea spawned out of mathematical intuition, similar things that have been proven, etc, that has not itself been proven. to prove this hypothesis would be to solve the problem. "proven". "proof". this is a weird concept, and something i never really got into. however, i will not let this hold me back from proving the riemann hypothesis.
i vaguely remember something from math class about riemann sums, which i later found out are actually related to the riemann hypothesis. a sum is...let me think back...i believe it's a succession of numbers, or algebraic constructs representing numbers, which go off, being added together, to infinity or towards some speficied bound. they have to start somewhere, too. unless they "start" at "negative infinity" (seriously).
i'm a little bit hazy on when a series is a sum, or vice versa. i think a sum is a series in which the terms of that series are added together, but i'm not sure how to notate that vs. just notating a series. or, any series might always be added up. i forget. so, forgive me if i use the terms "sum" and "series" in a muddled way. i think "sum" might be short for "sum of a series". i digress.
here's a popular example of a series:
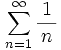
note the squiggle, which is the greek letter "sigma". it simply says to us: "this is a series." no need to be intimidated by it; it's full of beans. the n represents what the instances of the series will be, and where they willl be. we plug integers into n (1, 2, 3, etc), starting where the bottom of that squiggle tells us. in this case, we're told to start the series at 1, as indicated by the "n = 1". the little infinity sign above the sigma tells us where we stop. next, we have the meat of the matter: 1 over (divided by) the number of times the series has advanced at a point. remember, it starts at "n =1", and goes on to "n = infinity", marching up by integers. so, we get 1/1, 1/2, 1/3, 1/4, etc.
if you illustrate that sum (not just "1/1, 1/2, 1/3, 1/4, 1/5", but "1/1 + 1/2 + 1/3 + 1/4 + 1/5"), things get clearer, and also demonstrate another fundamentla concept. because i was weened on a graphing calculator, i think of everything visually (i often used to wonder about calc in the 19th century, and how kids wrapped their minds around it back then).
anyway, for instance, the sum of 1/n where n increments by 1 (1/1 + 1/2 + 1/3 + 1/4 + 1/5, etc), starting at 1 and going on forever, keeps getting bigger and bigger as n gets bigger. however, it keeps getting bigger by smaller and smaller amounts -- every time it gets bigger, it gets bigger by less. here, i'll draw an example of a series advancing towards a limit (not a precise physical representation of the series we were just talking about, but close enough -- this one is actually 1 + 1/2 + 1/4 + 1/8 + 1/16 etc.):

you can think of that uppermost line that the seems to be where things are stopping as representing a number, and the boxes as representing the terms of the series. as the sum of the series gets bigger, it will get close to that number, in fact "infinitely close," but will never reach it. the place it will never reach is called the "limit". it's considered to be the most essential concept in calculus, i believe, other than the "fundamental theorem of calculus", which is hard to draw. i used to find limits to be philosophically exciting, for some reason, probably because i was overly romantic/insane/a dweeb.
do you like how i avoid trying to prove the riemann hypothesis by giving you a rudiments lesson? but really, it's good for (my) understanding the riemann hypothesis, which is based on a certain series. i wish my first question had been something along the lines of "what's your favorite color?" maybe this will make a good break-in.
i enjoyed a somewhat shameful little flirtation with math, but i swear to you that it wasn't math affectation ("look at me, i'm smart, i'm taking math, etc"). some freshmen are unduly proud that they're taking calculus, it seems. i guess i was too -- but that wasn't the reason i was into math for that brief time.
the reason was that i was rather deeply moved by an intermediate algebra class in community college. before then, i never found math to be even remotely interesting, and i was bad at doing it by the rote that's required of the uninterested, just because i would make so many careless mistakes, not to mention never do my homework or study for tests. i was a math delinquent.
reasons i suddenly became good at math have been suggested: 1) i had a really good teacher. 2) my brain injury, having bashed up my right brain, had somehow awoken the left side, which was into math. 3) i was older, and took school more seriously. probably a combination of these and other unconceived factors.
fueled by this inspiration, i went on with math, through pre-calc, differential calc, and integral calc. i found it all exciting and cool, and i even went so far as to say there was some spiritual significance to it -- some kind of order to the universe and existence, knowledge of the infinite, etc etc. i'm not sure i ever expressed exactly how i felt. but i was positive, absolutely sure, that i was going to be a math major. little did i know that the classes got harder.
later, my feeling largely became that math was inspiring because it's fun to solve meaningless little puzzles comprising manipulated symbols -- completion, solution, a "right answer," the universe making sense, if only for an instant and in this ridiculous microcosmic model, is attractive and appealing. it gives a feeling of power and control. it's no secret that geeks are control freaks.
some of these puzzles correspond to some real, observable phenomena in physics that generally make civilization possible ("applied math"), but i didn't care about that -- in fact, i was disdainful of applied math. but, now, i'm starting to suspect that the only point of theoretical math is bring about unfortold future applications. and, to keep people like that old version of "me" happy to attend college.
i came out of integral calc with a "B" and, ironically, a very incomplete knowledge of sums and series. the riemann hypothesis has to do with a special case of a particular function containing a series. a function is a process -- something you do to a particular thing, no matter what that thing is, which yields a unique result for every different thing you "plug into" it. anyway, i decided that i was ill-prepared for multivariable calculus, and went off to go be a psychology major or something.
so, all of this math business lasted about two years, and i've forgotten almost all of the rigor behind it. in actuality, for a long time after math in large part had faded for me, i joked about taking only this knowledge from a year of calculus: how to make pretty integral symbols. but now, i've forgotten how to do even that. i know it's like an S, but i can't remember if it's backwards or forwards. oh yeah...forwards, and stretched out, top to bottom.
i'm going to have to load up wikipedia and research the riemann hypothesis a bit before i attempt to solve it for humanity, and collect $1,000,000 from the clay mathematics insitute, which i will of course split with whoever asked me this question.
Prove the following:
The real part of any non-trivial zero of the Riemann zeta function is 1/2.
there's a whole new wikipedia article for the riemann-zeta function, and it's slightly longer than the one on the riemann hypothesis. the riemann-zeta function is basically a series of complex numbers. a complex number is one that includes as a component the square root of negative one, which is amusingly called an "imaginary number." dave barry (or a similar entity) gave examples of imaginary numbers as "eleventeen" and "thirty-twelve." anyway, this hypothesis is defined as any example of the "dirichlet function" (which happens to include a series) where the function variable is any complex number where the "real" part (every complex number consists of "i", or the square root of negative one, plus some other quantity of a normal, or "real," number) is bigger than 1. anyway, here's the dirichlet series:
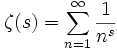
let me try translating the dirichlet series into english: for every instance in the series of one to infinity of our mystery number, that number is equal to 1 divided by the number by which that series has increased at that point (n) to the power of S, or the mystery number to begin with.
so, keep this in mind, and imagine that S is a complex number (an imaginary component plus a real component) where the real component does not equal one. that's the riemann-zeta function: a dirichlet series with particular values of its S (namely, complex ones with the real part NOT being 1).
the riemann hypothesis is concerned with the "zeros" of the reimann-zeta function, when plugging complex numbers into S. a "zero" of a function is a number, when plugged in, that causes the function to equal zero. if you plug in all of the complex "zeros" (we deal here only with compex numbers) you know into the reimann-zeta S, making sure you don't use 1 or negative even integers for the real part (i explain "why not" in the next paragraph), then the real part of any "non trivial zero" is probably, most likely, $1,000,000 says so, we hope, always going to be 1/2. that's the riemann hypothesis.
in other words, any complex number that you plug into riemann-zeta, which zeros the function, must have a real part of 1/2. complex numbers using negative even integers for their real parts will zero (verb) the function, but we don't care, because these are "trivial zeros." in other words, they don't refute the riemann hypothesis, because they've been known and understood for so long and are so "basic" that we don't consider these zeros in our hypothesis. even if you think this is lame, it's still the rules:
The real part of any non-trivial zero of the Riemann zeta function is 1/2.
...and it happens to be extremely likely to be true, but what no one (until me) has been able to prove, mathematically.
aren't you gratified that you read this far along?
without further ado, here is my proof of the riemann hypothesis:
stay up all night coming up with complex numbers whose real parts are equal to 1/2. plug one in the riemann-zeta function, and note that it zeros the function. plug another one in, and note same. repeat. etc.
after the function zeros for the 10,000,000th time, do you really, honestly think it's worth checking it for the 10,000,001th time, just to make sure it doesn't suddenly fail to happen? are you the kind of guy who believes that just because the sun has risen umpteen times in 5 billion years it won't necessarily rise tomorrow? what happens to your purse in vegas, man? this is what nietzsche calls the "absurdly rational." c'mon, people.
QED.